A Beginner’s Guide to Self-Supervised Classification

As of now, the self supervised learning procedure can be considered as making the data meaningful for the models that can perform the required task on the data. We can make the data structure more specific to the task to obtain more accurate results. In this article, we are going to discuss self-supervised classification where for the classification as a specific task, our need is to make the data more appropriate for the classification. The major points to be discussed in the article are listed below.

Table of Contents

1. What is Self-Supervised Classification?
2. Mathematics Behind the Self-Supervised Classification
3. Self-Classifier – A Self-Supervised Classification Network 

What is Self-Supervised classification?

If the classifications on the data are performed by the representation and label learned using self-supervised learning, it can be considered as the self-supervised classification. More than this definition, we can say that it is the process of making data for more accurate classification using the self-supervised learning process. Let’s discuss it in more detail while starting with self-supervised learning. 

As we know that, using self-supervised learning, we can make a machine to learn from the unlabeled data and also we can say that it is a somewhere intermediate form between supervised and unsupervised learning. Let’s take an example of natural language processing where if self-supervised learning is used, we can make machines learn a meaningful representation of the data without any human-provided label. 

More formally, we can say that the basic self-supervised learning methods are focused to learn the representation of the data and after learning the representation we can transfer them to downstream tasks like sentiment analysis and image classification. Basically, this downstream task is a predefined and simple one. When we talk about self-supervised classification, we can say that this process can be capable of performing various downstream tasks. 

Let’s say the learning model has learned that there are C classes in the data and now the task is to make a classifier that can classify the two augmentations of the data similarly. By this intuition, we can say that these classifiers are provided with a task that is prone to degenerate solutions where the samples of the data are related to the same class. The trivial solution can be avoided by editing the loss functions such as prior on the standard cross-entropy loss function.  

As we have discussed that self-supervised learning methods are a combination of the supervised and unsupervised learning methods, similarly the self-supervised classification can be considered as the combination of deep unsupervised clustering and contrastive learning. Here, the parameters of the assigned neural network and class assignment to the samples of the data can be learned simultaneously. 

Image source

The above image is a representation of a self-supervised classifier structure where a pair of shared networks are processing the augmented version of a similar image. Where we can see that the cross-entropy for every view is minimized so that the model can promote the same class prediction and assertion of the prior can avoid the degenerated solution. Using the same architecture we can learn the representation of the data and class labels in a single-stage end-to-end unsupervised manner.  

More formally we can say that this method is a combination of contrastive learning and deep unsupervised learning. Where contrastive learning is an approach of supervised learning and deep unsupervised learning is part of the unsupervised learning approach and in the self-supervised classification, it can help for learning the parameters of neural networks and also it helps in learning the cluster assignment of the final features using the unlabelled data. To understand it more, we are required to discuss the mathematics and logic behind the self-supervised classification.

Mathematics Behind the Self-Supervised classification

In the last image where the architecture of the self-supervised classification is explained, we have seen that we have two augmented views of the image as x₁ and x₂ and the goal of the method is to learn a classifier y_i , f(x_i) ∈ [C]. 

We can consider that C is the number of classes and f(.) is the function which the classifier follows and the downstream aim is to classify views similarly if the views are the augmented version of each other and also make the classifier to be capable of ignoring the degenerate solutions. A common way to learn using a multiclass classifier is by minimizing the loss function and if the function as loss function is cross-entropy loss function then the minimization can be done by 

Here, the row softmax is p(y|x), and if we are trying to minimize the above-given function without additional regularization, we can have degenerate solutions. To avoid the degenerated solutions, we can introduce the Bayes theorem on the loss function as:

Dropping the denominator and controlling the prior p(y) can help in the regularization of the solution. By asserting a uniform prior on y we can use all the classes of the data. The resulting loss will be:

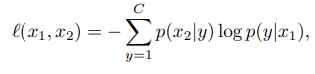
In the above-given formula, the p(x|y) is a column softmax whose symmetrized version will be:

Where the prior is very important because without a uniform prior the solution will provide a very nonuniform p(y). All the samples from the data will get assigned to a single class.

So in the above section, we have seen what procedure can be called as a self-supervised classification and what can be the mathematics and logic behind the self-supervised classification. In the next section, we are going to have an overview of a package self-classifier that allows us to use the models based on self-supervised classification. 

Self-Classifier – A Self-Supervised Classification Network

Self-classifier is a self-supervised classification neural network that helps in learning the representation of the data and labels of the data simultaneously in one procedure and also in an end-to-end manner. The python implementation of the Self-Classifier’s pre-trained model can be found in the link. In the architecture of the package we can see that using the convolutional layer and fully connected layers the models under the package can learn representation and class labels. 

In this section of the article, we are going to discuss the comparison of the self-classifier with other methods, models and packages so that we will know the importance of self-supervised classification. 

Elad Amrani, IBM Research AI, Technion, and the team have developed the package. The developers of the package say that the self-classifier is simple to implement and details about how to implement this package can be found in the link. Unlike other state-of-the-art methods, it does not require large memory or any other second momentum neural networks. Clustering and classification tasks can be performed by a single package. A comparison between some of the famous state of the art models and Self-classifier following the architecture of ResNet-50 for image classification is listed below., 

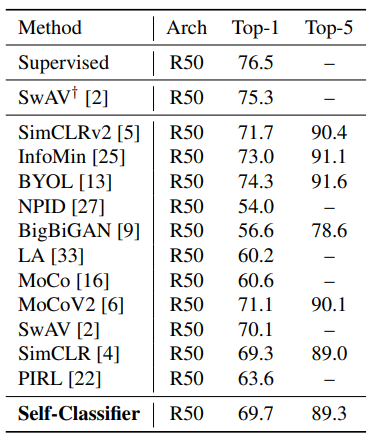
The example we have taken is mainly useful for the image classification task with a very light framework enabled and also very easy to use. The architecture we have seen is just to make the data representation meaningful and classes labelled so that it can be classified easily and accurately. 

Final Words

Here in the article, we could understand how we can define the self-supervised classification from the self-supervised learning domain of machine learning. We have also seen a proposed way of logic and mathematics that can play a crucial role behind the self-supervised classification models. Along with that, we have gone through an example of it named Self-Classifier with its comparison to the other traditional methods.