In recent years, we have seen that graph embedding has become increasingly important in a variety of machine learning procedures. Using the nodes, edges, and other components of the graph embedding, we perform a variety of tasks like clustering, PCA, classification, etc. in a very robust manner. In this article, we will discuss graph embedding in detail with its mechanism and applications. The major points to be discussed in this article are listed below.
Table of contents
- What are embeddings?
- What is graph embedding?
- Nearness function
- Advantages
- Application
What are embeddings?
In mathematics, if any instance is contained within another instance of some mathematical structure, it can be considered as an embedding. For example, the subgroup of a group. When we talk about in the context of machine learning, embeddings are low-dimensional, learned continuous vector representations of discrete variables into which we can translate high-dimensional vectors. Using the embeddings, we make machine learning models more efficient using these representations of data. Also, these embeddings can be used with other models.
Generally, we see the use of embeddings in NLP applications where embeddings can be considered as a technique of mapping words into vectors that can be modelled and analyzed better. For example, Maruti and Nexa words are hard to relate for a machine but in vector representation, we can set these words close according to some measure. The embeddings can be used in various machine learning tasks like making recommendation systems, text modelling, graph modelling, etc. We can categorize embeddings in machine learning according to dimensionality and purpose of usage. It can be n-dimensional and also it can be either word embedding or graph embedding. In this article, we are going to discuss graph embeddings.
What is graph embedding?
As we just discussed, embeddings can be the subgroups of a group, similarly, in graph theory embedding of a graph can be considered as a representation of a graph on a surface, where points of that surface are made up of vertices and arcs are made up of edges. By this, we can say that a graph embedding can have the following characteristics:
- The endpoints of the arc are associated with an edge.
- Edge is the points associated with the end vertices of that edge.
- Arc has no points that are associated with other vertices.
- Two arcs never intersect at a point that is associated with either of the arcs.
Embeddings can also be considered as a drawing of the graph on the surface where the surface is compact and connected by 2 manifolds. Also, one thing that is important about the graph is that ridges intersect only at their endpoints.
We can also say that we use graph embedding for finding the latent vector representation of the graph that captures the topology of the graph. Latent vector representation in a graph embedding includes vertex-vertex relationships, information of edges, etc. There can be two labels of embeddings in the graph:
- Vertex embeddings: Vector representation of vertices of the graph can be found in these embeddings. Comparison between vertices can be done by mapping these vectors in the space and the mapping we can find that the similar vertices of the graph are mapped closer than the other different vertices.
- Graph embeddings: Representation of the whole graph in the form of latent vectors can be found in these types of embeddings. For example, from a group of compound structures, we can extract similar compounds and types of compound structures in the group using these kinds of embeddings. We just need to map these structures in space and calculate the information.
We can also understand the graph embedding using the following points:
- Graph embeddings are a type of data structure that is mainly used to compare the data structures (similar or not).
- We use it for compressing the complex and large graph data using the information in the vertices and edges and vertices around the main vertex.
- We use machine learning methods for calculating the graph embeddings.
- We can think of embeddings as a low-dimensional representation of the data in a vector space.
- it is a way to solve the fuzzy match problem using small codes and low maintenance.
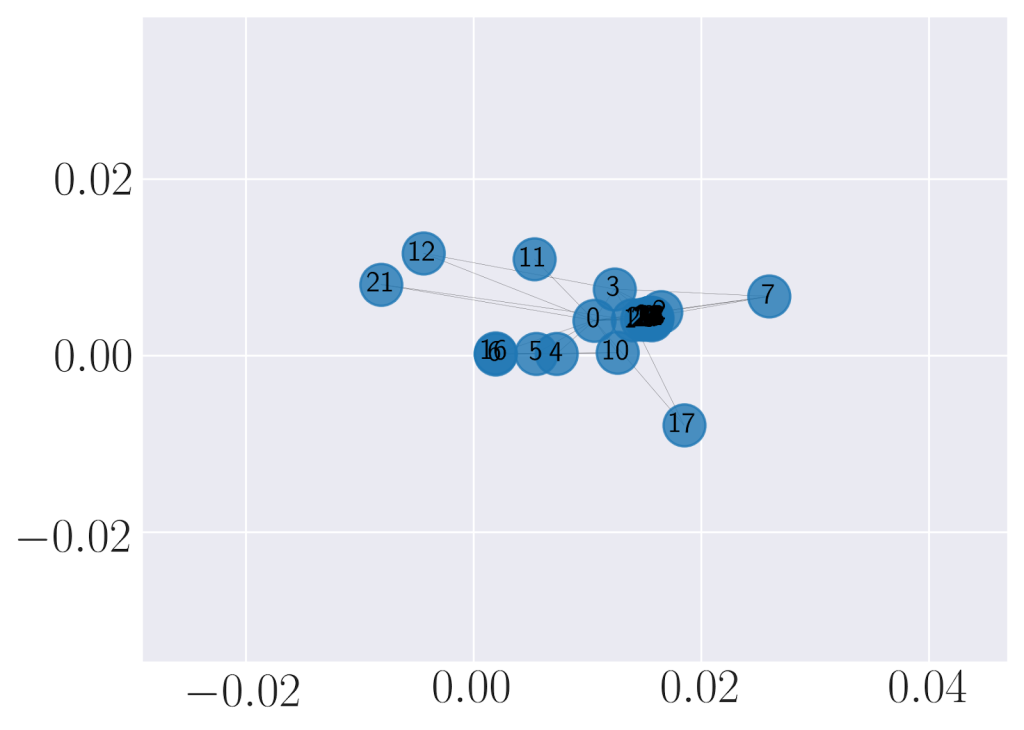
The above image is a representation of graph factorization of karate graph embedding. As we have discussed, these embeddings are used to find the similarity between graphs. This similarity can be found using the nearness function. Let’s describe the nearness function.
Nearness function
Given two points in the space, we can calculate the distance between two points using the Euclidean distance formula as given below:
The above image represents the coordinates of two points in a two-dimensional space. In graph embedding, we use the same method for calculating the distance in a complex way where we may have complex dimensionality space. Finding the distance between embeddings causes the measure of similarity between embeddings.
Where did it all come from?
As far as we can see in the past we can find that the works related to the graph embeddings come from the world of natural language processing. Where in NLP by finding the distance between words or phrases researchers trained the network to perform various tasks. To understand the working of these embeddings we are required to understand how word2Vec works.
Let’s say we have words like man, woman, king, and queen and we mapped it in a two-dimensional map where the x-axis relates the words, man and woman. The Y-axis relates to the royalty state. In such a scenario the king will be close to the man and the prince will be close to the king in the royalty gender space.
The English language has almost 40,000 words and manually scoring these words is difficult so we use machine learning models to score them. We can train a network to calculate the embedding for each word. This is a general Word2Vec procedure. Using a knowledge graph we can create a pair-wise link between each word and every other word. Weights of the link can be considered as the distance of the word. This approach is a fast and easy way to calculate the similarity.
Advantages
As of now, we have seen what graph embedding is and what is the reason behind the origin of it. The advantages of graph embeddings are as follows:
- Choice of property: Forming a good graph embedding provides us with a good representation of nodes in the form of vectors. Also, it preserves the structure of graph data and the relationship between the nodes.
- Scalability: As we can see in recent times, the networks are complex and contain a huge number of nodes and edges. Embedding them provides a scalable property using which we can process large graphs. Using embedding we can easily define a scalable model that is aimed to preserve the whole properties of the network.
- Optimal dimensionality: Using it we can find optimal dimensions of the representation of the graph. The dimensionality of the embedding can be according to the application.
Application
The popular applications of graph embeddings are listed below:-
- It can be applied to recommendation systems that have interests in social networks. By extracting the vertex embeddings, we can find similar entities(persons) and recommend them to the same products.
- It is a better way to deal with adjacency matrices because a graph has an adjacency matrix where its dimension can be in millions and latent graph embedding dimensions are very less than the adjacency matrix. By using a product of adjacency and dimensions of latent embedding we can make the graph easy to process.
- One of the most common applications is in natural language processing. We can replace the Word2Vec procedures with the graph embeddings to maintain and increase the robustness of the models and procedures.
- Since it has the property of being compact we can use it for dimensionality reduction problems by converting the data into graphs and then graph embeddings.
- Vectorization of the graph data can be done. We mostly find this type of work on social networks. In which peoples in the network can be considered as vertices and edges representing the connection in the graph of the social network.
Final words
In this article, we have discussed graph embeddings where we got to know its advantages and its origin and how it works. Along with this, we have also gone through some of the applications of graph embeddings in machine learning procedures and social media.